量子コンピューターは無限の計算能力を手に入れるか？

2019年10月31日 17:43

　Google の量子コンピュータの超越性の記事をきっかけにブロックチェーンや仮想通貨の安全性の話に飛び火し、ビットコインの価格が大きく動いた。現時点ではまだまだ実用段階ではないということは、すでにいろいろなところで語りつくされているだろう。

　しかし量子コンピュータと暗号については私は前々から思っていることがあった。いい機会なのでそれを語ってみたい。今回は物理学的な考察が入っている。なのでいつにもまして眉唾で読んでもらいたい。

地球の全情報を割りバシに刻む方法

割りバシ

　地球の文化や科学技術を調査しに来た宇宙人が3年間かけて収集した情報（500エクサバイト）を割りバシ一本で持ち帰るという小話があった。やり方は簡単だ。その情報を10進数で書き表す。67281920012873・・・といった感じで。書き終わったらおもむろに先頭に０．を書き加える。
　これで 0.67281920012873・・・となった。あとは割りバシの長さを1としたときのこの割合の場所に印をつけるだけでいい。母星に戻ったら割りばしの長さと印の位置を測って割り算をすれば元の情報を復元できる・・・。

　もちろんこれはうまくいかない。割りバシは炭素原子で出来ており、どんなに頑張っても１オングスロトーム程度の解像度でしか印をつけることができないからだ。割りバシの長さについても原子レベルで見れば激しく動いており長さの精度さえ限定的だ。このケースだと５００エクサバイトどころか１キロバイトだって表現できないだろう。

バナッハ＝タルスキーの定理

バナッハ

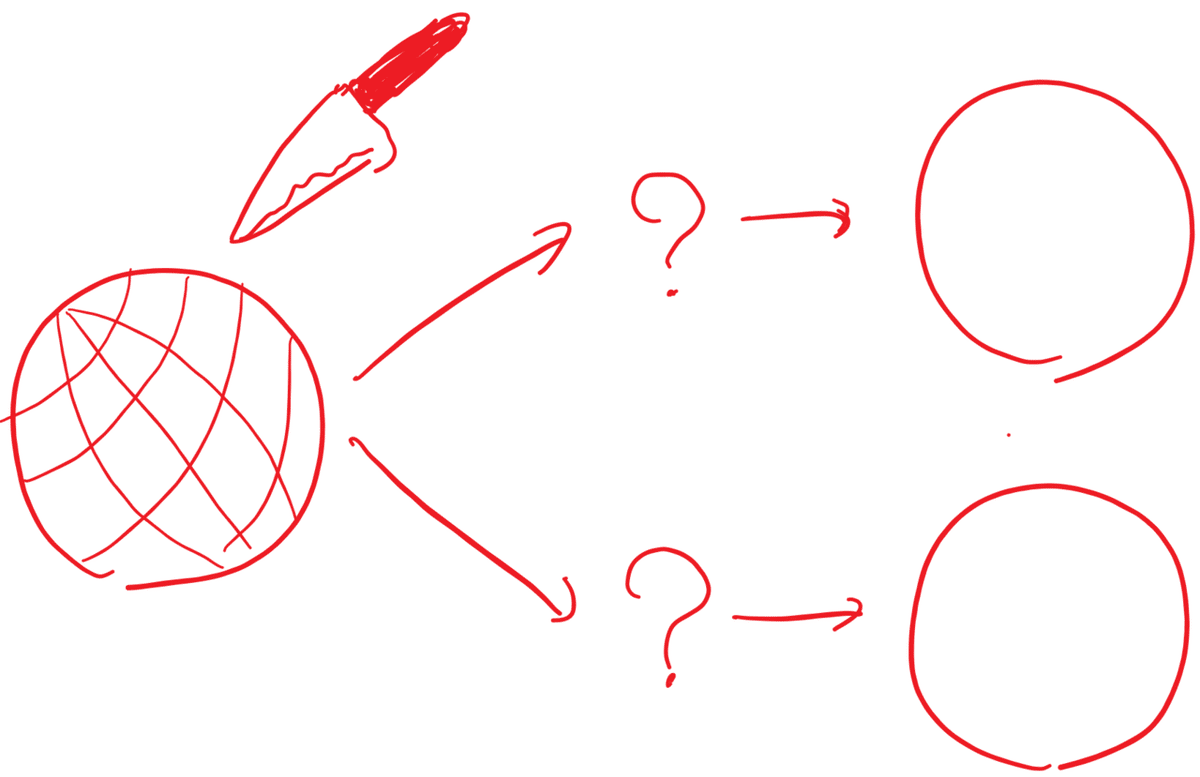
　中身の詰まった球体を考える。この球体を有限個のパーツに分割して、再び組み合わせて元の球体と全く同じ大きさの中身もちゃんと詰まった２つの球体を作ることができるだろうか？

　もちろん不可能だと思うだろう。しかしバナッハ＝タルスキーの定理はそれが可能であると主張する。証明もちゃんとある立派な数学の定理だ。

　このカラクリはこうだ。有限個のパーツには分割するのだが、分割の仕方に種がある。この分割の仕方とは、切断面がある意味無限にギザギザになっているのである。だから偶数の数と自然数の数が一致するのと同様、再び組み合わせることで元の球体が２個複製できてしまうのである。

　もちろんこれは現実には実現不可能だ。どんな物体も無限にギザギザに加工できないからだ。だから質量保存の法則は破られることはない、よかったよかった。

量子コンピューターで楕円曲線暗号を破る方法

　さて何の話をしているのか脱線しまくってすまない。ここから量子コンピューターの話にもどろう。
　まずは量子コンピューターがどのように動くのか、動作原理を説明しよう。アルゴリズム自体はいろいろ小難しい話が出てくるが本質的な部分は結局のところ次のような方法だ。

　ビットコインの鍵長は２５６ビットなので、同様に２５６量子ビット（キュービット）を用意する。
　次にこの２５６キュービットをエンタングルメントさせて、１～２の２５６乗までの重ね合わせ状態にする。
　あとは重ね合わせ状態をキープしたまま楕円曲線の演算を行い、「量子フーリエ解析」という謎メソッドにぶち込む。
　最後に重ね合わせ状態にある２５６キュービットを観測して状態を収縮させることで解を得る。

　現状では２５６キュービットも用意できないし、十分にエラー率の低い演算を行うこともできていない。あるいは汎用演算をすることにも困難がある。まあなので今のことろ騒ぐほどのことではない・・・というのが今のところ主流な意見だろう。

結局楕円曲線暗号は破られるの？

　しかしそれは問題を先送りにしているだけだ。だったら十分に技術が進化したらどうなるのだろうか？

　そもそも暗号技術はコンピューターが進化したら鍵長を増やす、という方法で対抗することを前提としている。だから十分な計算能力を備えたコンピューターが現実的になったら鍵長を５１２、１０２４と増やしていくのが従来の考え方だ。
　だから量子コンピューターも同じなら何も騒ぐようなことではない。将来にわたって今までと同じようにコンピューターの進化に合わせて鍵長を増やしていけばいいだけのことだ。

　ムーアの法則が生きていたころは過去になり、現在は古典コンピュータには物理的な限界があると考えられている。演算速度を上げるには集積度を上げるしかないが、割りバシの話と同じく最後は原子の大きさの話になってしまう。あるいは不確定性原理の限界にはまってしまう。だから古典コンピュータを相手にしている限り、ここしばらくは演算能力の絶え間ない進化、ということを忘れていただけだ。

　量子コンピューターにはその限界がないのだろうか？
　もし限界がなく、簡単にキュービットを増やすことができるなら、楕円曲線暗号を含む公開鍵暗号は破られたといっていいだろう。いつの日かそのような日が来たら何かほかの仕事を始めよう。

　一見キュービットを増やすのは線形に行えるように見える。今はまだ技術が追い付いていないだけで、１０２４どころか１億キュービットも、いずれ可能になるのではないかと。

　本当にそうだろうか？動作原理の説明で「次にこの２５６キュービットをエンタングルメントさせて、１～２の２５６乗までの重ね合わせ状態にする」と書いた。
　言い換えれば１０の７７乗個の重ね合わせを作るということだ。１０の７７乗個といえば観測可能な宇宙に存在する粒子に匹敵する。ホントに波動関数はこんな驚異的な精度を表現できるのだろうか？
　いやもしかしたらできるのかもしれない、真の疑問はこうだ。２５６の次は５１２だ。そうすると１０の１５０乗を超える。波動関数はこんな驚異的な精度を表現できるのだろうか？
　いやそれさえももしかしたら行けるのかもしれない。正しい疑問はこうだ。これはどこまで続けられるのだろうか？

　物理学の歴史は「世の中には原理的に離散的にできている」ということを発見してきた歴史でもある。
　ほかならぬ量子力学が長さの最小精度、エネルギーの最小精度などをプランク定数を使って暴いてきた。ループ量子重力理論などでは時間にも最小単位があるという。一定の空間領域に詰め込むことのできる情報量はその領域の表面積に比例するという理論もある。

　波動関数の重ね合わせがどこまで可能かはまだ判明していないと思う、というかそんなこと考えていないだろう（この辺は素人なのですでに理論があるなら全力で撤回します）
　しかし評論家気取りで予測するなら、ここにも限界があると思う。量子コンピューターの研究はその限界を明らかにしていくのだろう。ムーアの法則と戦ってきたエンジニアたちと同じように。

　しかし逆に多世界解釈のような世界観が正しく、波動関数はいくらでも重ね合わせ可能なのかもしれない（多世界解釈なら重ね合わせではなく、世界のほうが分岐しているわけだが）
　そうなれば、その時は予想が外れたわけであるが、SF的には非常にワクワクする展開だ。私は無神論者だが、もし物理法則が無限に近い演算能力を黙認するのなら、そこに神の存在を感じることができるに違いない。