
パッティングの物理
結論から申し上げますが、私はゴルフのパッティングにおいてのグリーンの傾斜に関する以下の方程式をご案内したいと思います。
調整距離(m)=2 * 傾斜角(°) * 距離(m) / 10 ・・・①

ここでは①をパッティング調整方程式と呼びます。ただし、これはボールが傾斜(ボールが転がる方向)とカップを結んだ線上にある場合をを想定しています。芝目は傾斜と比べると小さな影響ですが今回は無視します。ボールがカップと傾斜に対して斜めに位置している場合は、いずれ考えてみたいと思います。
・傾斜角はグリーンの傾斜角度を度で表記
・距離はボールからカップまでの距離

仮想カップを考えよう!
実際のカップの位置に対して、グリーンの傾斜による影響を考慮して強弱を付加してパッティングをするかと思います。水平なグリーンでその強さで打ったときにあるカップの位置を「仮想カップ」と呼びます。
仮想カップ = 距離+調整距離 ・・・②
ゴルフのグリーンの傾斜は1°から4°が主な角度。これ以上急な傾斜は部分的な場所以外にはあまりないかと思います。それは急な角度は自重でボールが止まってることができずに、カップに入れることが非常に困難になるからです。パチンコのようになってしまいます。
iPhoneに最初から入っている「計測」というアプリで傾斜が測定できます。実際に計測してみると分かりますが、1°の違いを人間は認識できると思います。グリーンでの4°はかなり急な傾斜と感じるはずです。
三角関数で高さを求めよう
それではなぜ①が成立するかをご説明いたします。
角度1度は1mの距離では1.7455cmの高低差を生む ・・・③
これは簡単ですね。タンジェント(tan)は三角形の底辺の長さに対する高さの比率のことです。tan(radians(1°)) = 0.017455 なので、底辺が1mで1°の傾斜だと1.7455cmの高さがあることになります。
またタンジェントは10°以下くらいの小さな角度については、角度と高さがほぼ正比例することが分かっています。例えば、tan(radians(4°)) = 0.069927 なのですが、これは4 * tan(radians(1°)) = 4 * 0.017455 = 0.069820 とほぼ近い値を取ります。
スティンプメーターとは
10cmの高低差で1mの距離の差を生む ・・・④
④ですが、ゴルフ場にいくと「本日のグリーンは8.5フィート」などの表記があると思います。これはスティンプメーターと呼ばれる機器(といっても、単なる金属の筒でボールを転がすだけ)で、グリーンの速さ(と呼んでいるが、実際には抵抗)を測定した結果を表示しています。
スティンプメーター
長さ36インチ(91.44cm)、縦方向に溝があり、先端のテーパー部分から約30インチ(76.2cm)のところに切り欠きがあるのが特徴です。ボールは、スタート地点で地面に平らに置かれ、もう一方の端を約22度の角度まで持ち上げると、重力によってこの切り欠きから放出される
では、斜辺が76.2cmで角度が22°の三角形の高さは何cmでしょうか?
sin(22°)ですね。ラジアンに直さないといけないので、76.2 * sin(radians(22)) = 76.2 * 0.3746 = 28.54cm
スティンプメーターを高さ28.54cmまで傾けるとボールが転がりだすということが分かります。

位置エネルギーと移動距離は高さに比例
さて、物理で習った通り位置エネルギーはmghで表せますね。mは質量。この場合はボールの質量。gは重力加速度、hは高さです。ボールの質量は変わらないので、位置エネルギーは高さに比例することが分かります。
この位置エネルギーがボールが転がる時の摩擦によって減少します。摩擦が0なら、ボールは無限の距離を転がります。芝の動摩擦係数が一定(厳密には変化する)だとすると高さが2倍になれば、2倍の距離を転がります。理由を以下に述べます。ボールの位置エネルギーはスティンプメーターの下端ですべて運動エネルギー(1/2*mv^2)になります。そして芝の抵抗がボールにマイナスの仕事をして最後は止まります。
F(芝の抵抗)*s(ボールの移動距離) = 1/2 * mv^2 = mgh
F(芝の抵抗)= μ'(動摩擦係数)* N(垂直抗力 = ボールの重さ = mg)
μ' mg * s = mgh
s = h/μ'
より、ボールが転がる距離はボールの高さに比例します。
一般的なゴルフ場の芝はスティンプメーターで9feet(2.7432m)くらいの値を取ります。0.2854mの高さに対して2.7432m転がるので、約1:10です。なので10cmの高低差で1m転がります。よって④の10cmの高低差で1mの距離の差を生むと説明できました。
※厳密には、0.2854mと1:10になる芝の速さは9.36feetです。そして、9 feetを基準にすると、0.2854mで9 * 0.3048m (2.7432m)進むので、10cmにつき0.9611mの距離の差を生みます。④'
パッティング調整方程式の完成
さあ、これでパッティング調整方程式が完成します。
高さ10cmで0.9611mの芝の抵抗は
高さ1.7455cm(1度で1mの距離の高さ)で0.1677mになります。
③と④’及びタンジェント正比例より、以下の方程式が導けます。
調整距離(m)=0.1677 * 傾斜角(°) * 距離(m)

覚えにくいので係数を0.2(=2/10)と簡略化して①が導けました。0.1677と0.2は19%しか違いません。グリーン上で二桁の暗算をするのは厳しいのと、傾斜は1度の角度の読み違いで100%値が変わってきて、こちらの方が影響が大きいです。そして、アマチュアにとって調整距離19%の誤差(例えば4.3mと4.55m)を打ち分けるのはほぼ不可能だからです。そして何より調整距離19%の誤差は、実際の距離の誤差でいうと更に小さくなりカップが吸収してくれます。なので、0.2を使うことをお勧めしています。(計算が得意な人は0.17を使用してください)
②の仮想カップまでの距離は、上りなら①を実際の距離に足し、下りは減らします。上りと下りで調整距離には差がありません。パッティング調整方程式はエネルギーと芝の抵抗による仕事のみで計算しているからです。後はこれで求められた仮想カップに打つような強さでパッティングすればカップインします。
最後にパッティング調整方程式で求められた調整距離の理論値を載せておきます。
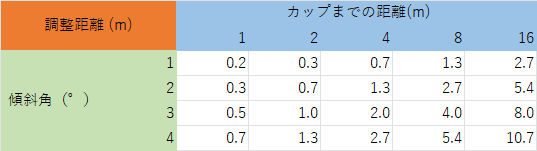
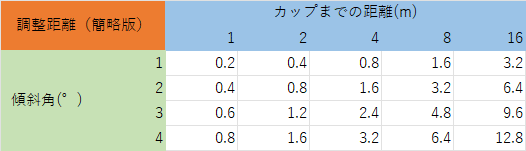
例えば、カップまでの距離が4mで傾斜角が3°の上りなら、6.4m(正確には6.0m)の力加減でパッティングすれば良いです。忘れてはならないのはこれはスティンプメーターが9 feetを基準としています。芝が10 feetの速さなら、調整距離を1.1倍してあげてください。
これで皆様もパッティングの力加減で悩むことはなくなりますね。
覚える数字はたった1つ。0.2(2/10)です!
パッティング調整方程式で皆様がスコアアップすることを願っています!
最後に、株式会社bitFlyer Blockchainでは仲間を募集してます!

